Probablemente en tu niñez más de alguna vez te planteaste la situación en donde te pusieras a contar los números consecutivamente o con algunas técnicas para avanzar más rápido en el conteo podrías llegar hasta el final de ellos, pero lo único que lograbas encontrar era una cantidad enorme que ni si quiera podías leer (o tal vez aún te es difícil poder leerla).
Después del desánimo obtenido lo que nos quedaba por concluir es que los números son infinitos. Pero hasta aquí solo hablábamos de números que son enteros y para ser más precisos naturales.
Al seguir avanzando en nuestros estudios escolares descubrimos los números racionales, irracionales y además los números negativos; en conjunto a todos estos los llamamos números reales.
Claramente esta amplia variedad corroboró nuestra idea de que los números son infinitos.
Todos estos números los utilizábamos por ejemplo en las operaciones básicas, determinar superficies, determinar áreas y muchas actividades más.
Tal vez el uso más impresionante que le encontrábamos en secundaria a estos números era solucionar ecuaciones lineales y cuadráticas. Quizás lo impresionante de las ecuaciones era causado por el trabajar en conjunto con letras y números.
Pero, ¿qué pasaba cuando nos topábamos con ecuaciones como la siguiente?
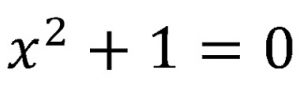
Al solucionarla encontrábamos que
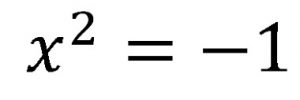
¿Es decir un número elevado al cuadrado que resultara negativo?
Seguramente enseguida tu profesor decía: “esas ecuaciones no tienen solución”.
Tal vez ya lo sepas, pero si no, te diré una gran verdad…
¡Todas las ecuaciones tienen solución!
Para dar solución a las ecuaciones de este tipo es necesario ampliar un poco más nuestro conocimiento de los números.
Llamaremos a estos números imaginarios.
Sí, imaginarios. Probablemente este nombre no te resulte muy convincente pero el matemático Leonhard Euler quien fue el primero en trabajar con ellos en 1777 y así decidió llamarlos.
La característica principal de estos números es el valor de:
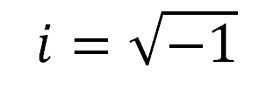
y de manera general se llamará el conjunto de números complejos a los que números que tengan la siguiente forma:
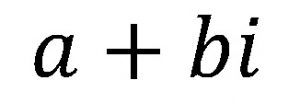
donde a y b son reales.
Este nuevo conjunto de números también tienen definidas las operaciones aritméticas y las propiedades que con ellas conllevan.
Podría sonar extraño que algo con el nombre imaginario tenga aplicaciones en la vida real, pero gracias a estos números se han llegado a grandes resultados científicos.
Menciono enseguida algunas aplicaciones.
- Asegura que se cumpla el teorema fundamental del álgebra, el cual dice que todo polinomio de grado n-ésimo tendrá n soluciones.
- Se utilizan para describir circuitos eléctricos y ondas electromagnéticas.
- Los fractales se les define a través de cálculos con números complejos en el plano.
- Por sus componentes reales e imaginarios se usan para facilitar el estudio de cargas sobre vigas, estudio de ondas, además se emplea en los estudios concernientes a la propagación del calor.
Estas son sólo algunas de muchas más aplicaciones que tienen los números complejos.
Así que ahora no solo juzgarás a un libro por su portada, sino que también, no juzgarás a las matemáticas y sus elementos aún por más curiosos que sean sus nombres.



































